Tversky Neural Networks: Psychologically Plausible Deep Learning with Differentiable Tversky Similarity

[📄 manuscript (under peer review)] [code (coming soon)]

What if neural networks assessed similarity like humans?

We introduce Tversky Neural Networks, based on Tversky's (1977) psychological theory of similarity. These models enable efficient, interpretable, and psychologically plausible deep learning.

The issue

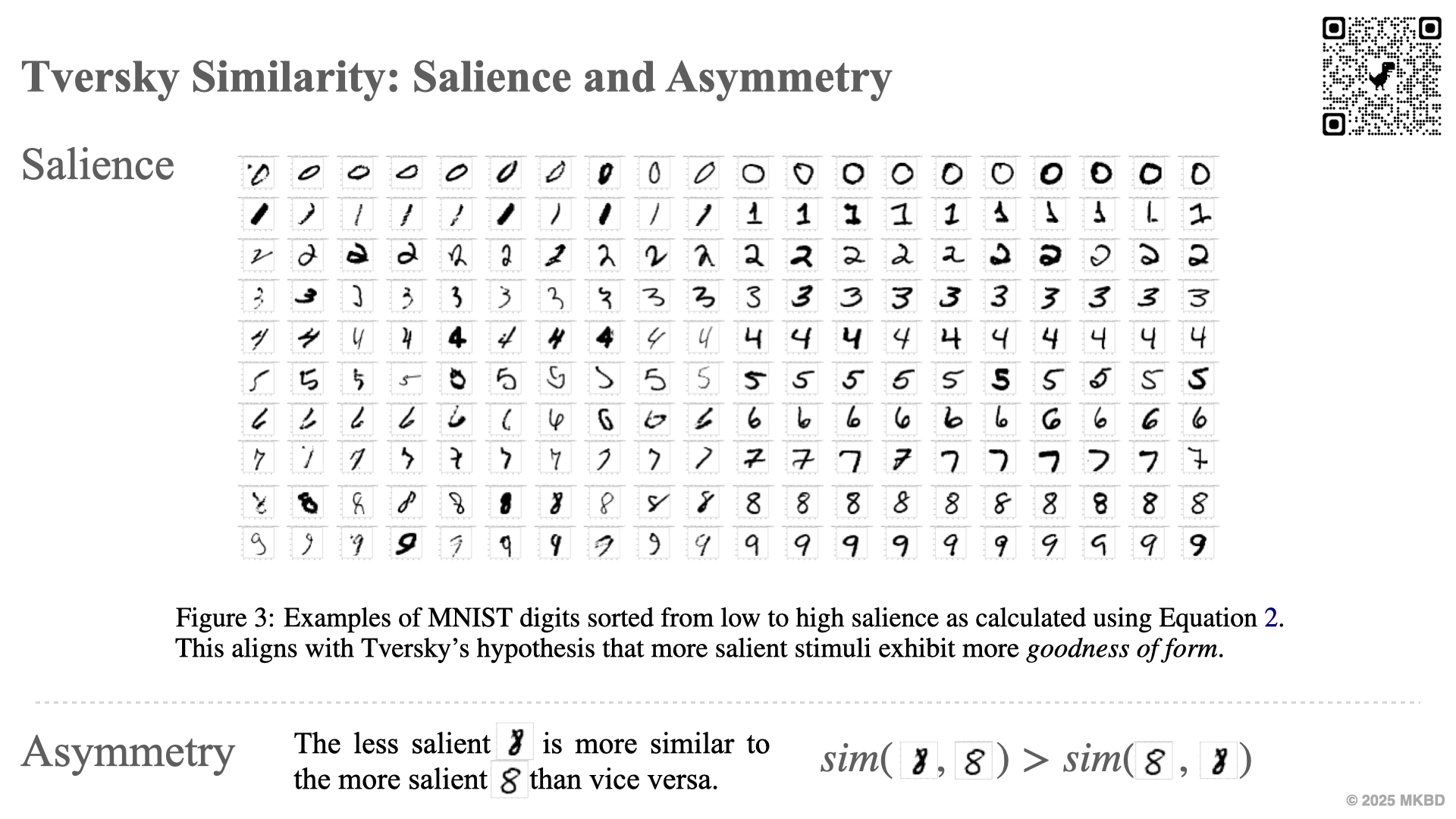
"The father is like the son" and "The son is like the father" differ. Humans violate properties such as symmetry while assessing similarity. Therefore similarity measures such as dot product, cosine and L2, which are symmetric and widely used in modern deep learning are incompatible with human cognition.

Our solution

Differentiable Tversky similarity, using dual representation of objects as vector and as sets, learnable via gradient descent. The similarity of one stimulus to the other is computed as a function of measures of the common and distinctive features of the stimuli, mirroring human cognition per Tversky's theory.

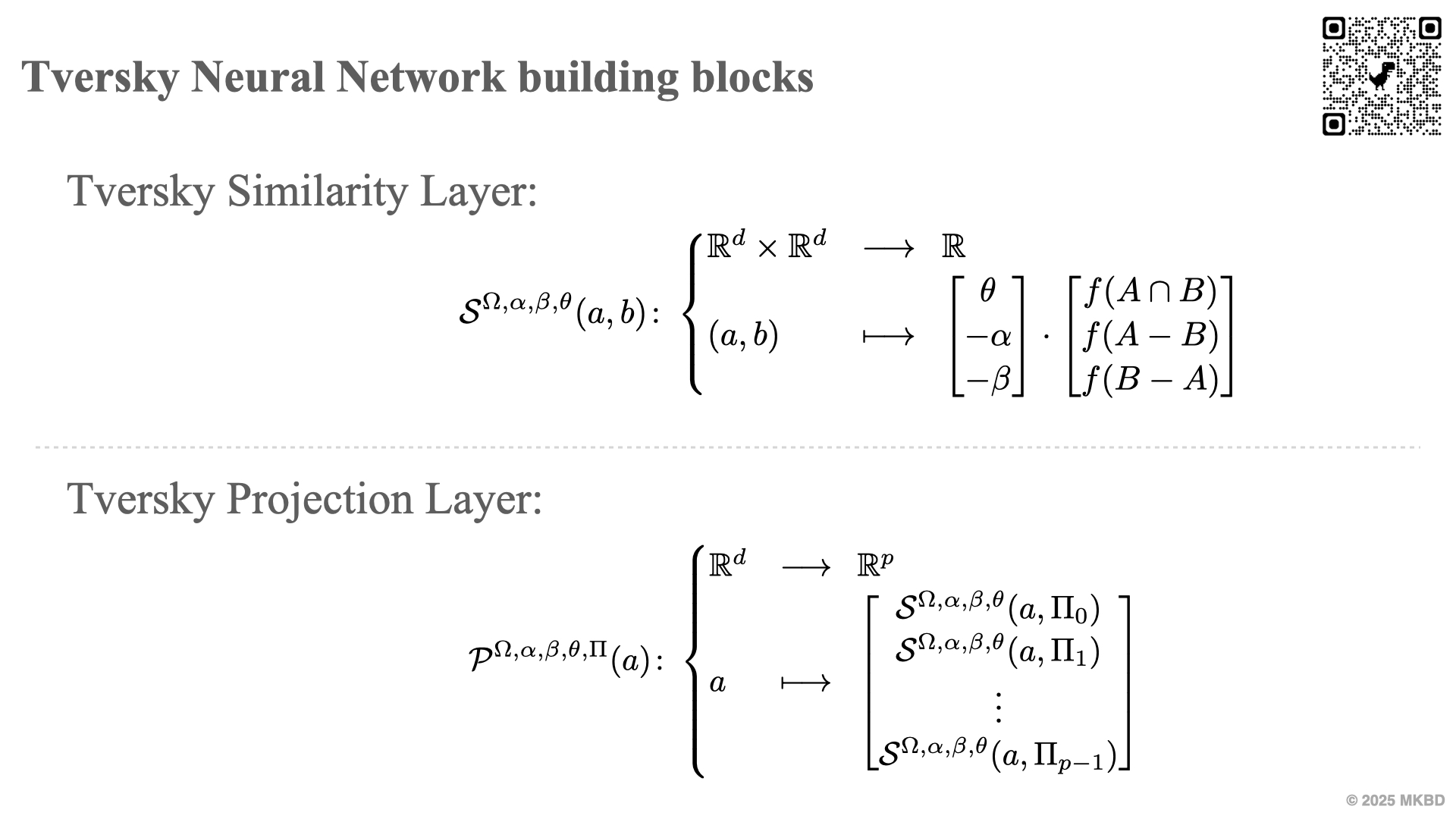
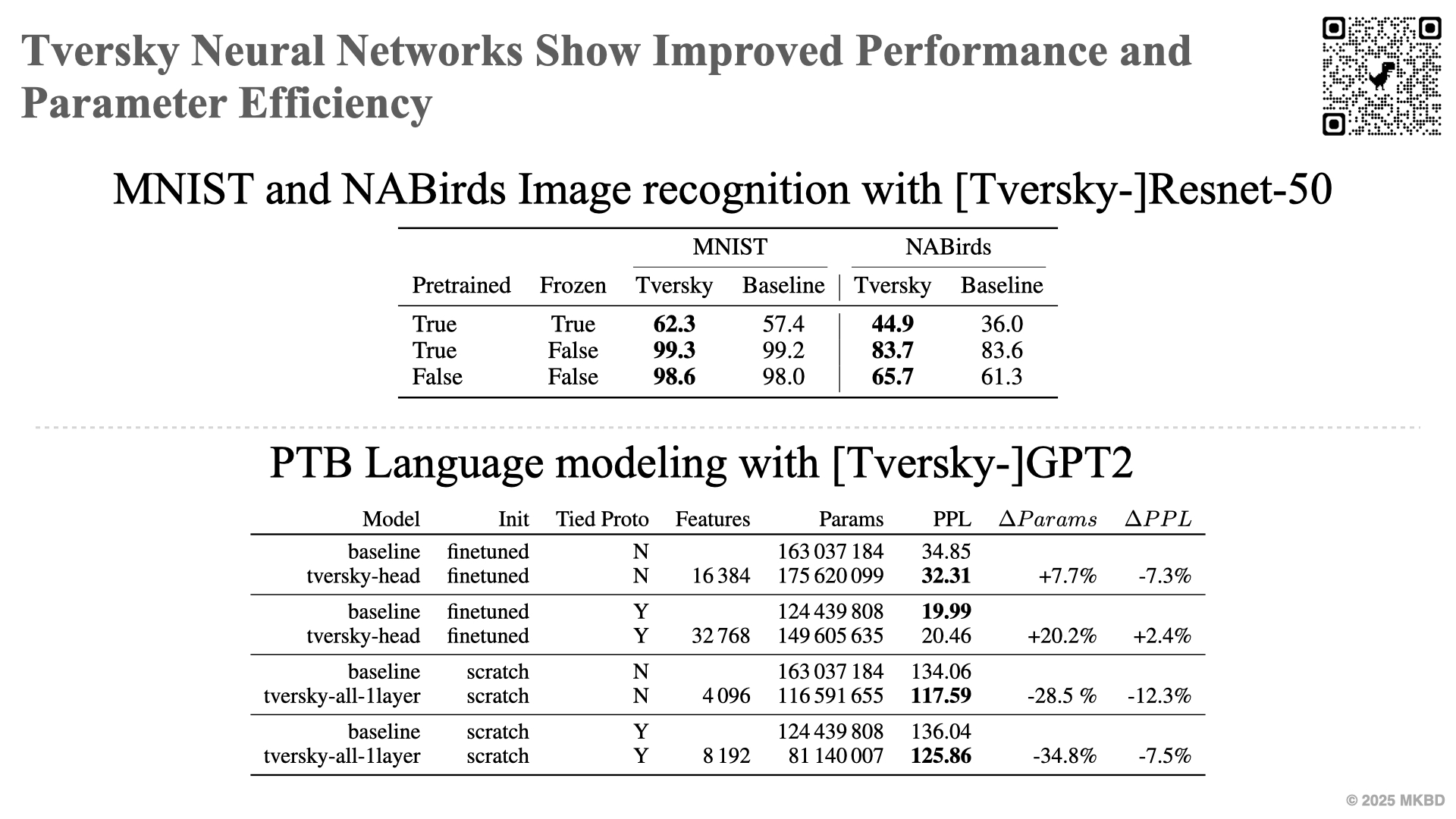
Tversky projection layers compute Tversky similarity of inputs to learned prototypes. They are a drop-in replacement for fully connected layer stacks. Our experiments on image recognition and language modeling with Resnet-50 and GPT-2 showed that replacing fully connected layer stacks with a Tversky projection can result in increased performance and parameter efficiency. Tversky projection layers also allow a configurable feature bank size, and interpretable feature sharing options.

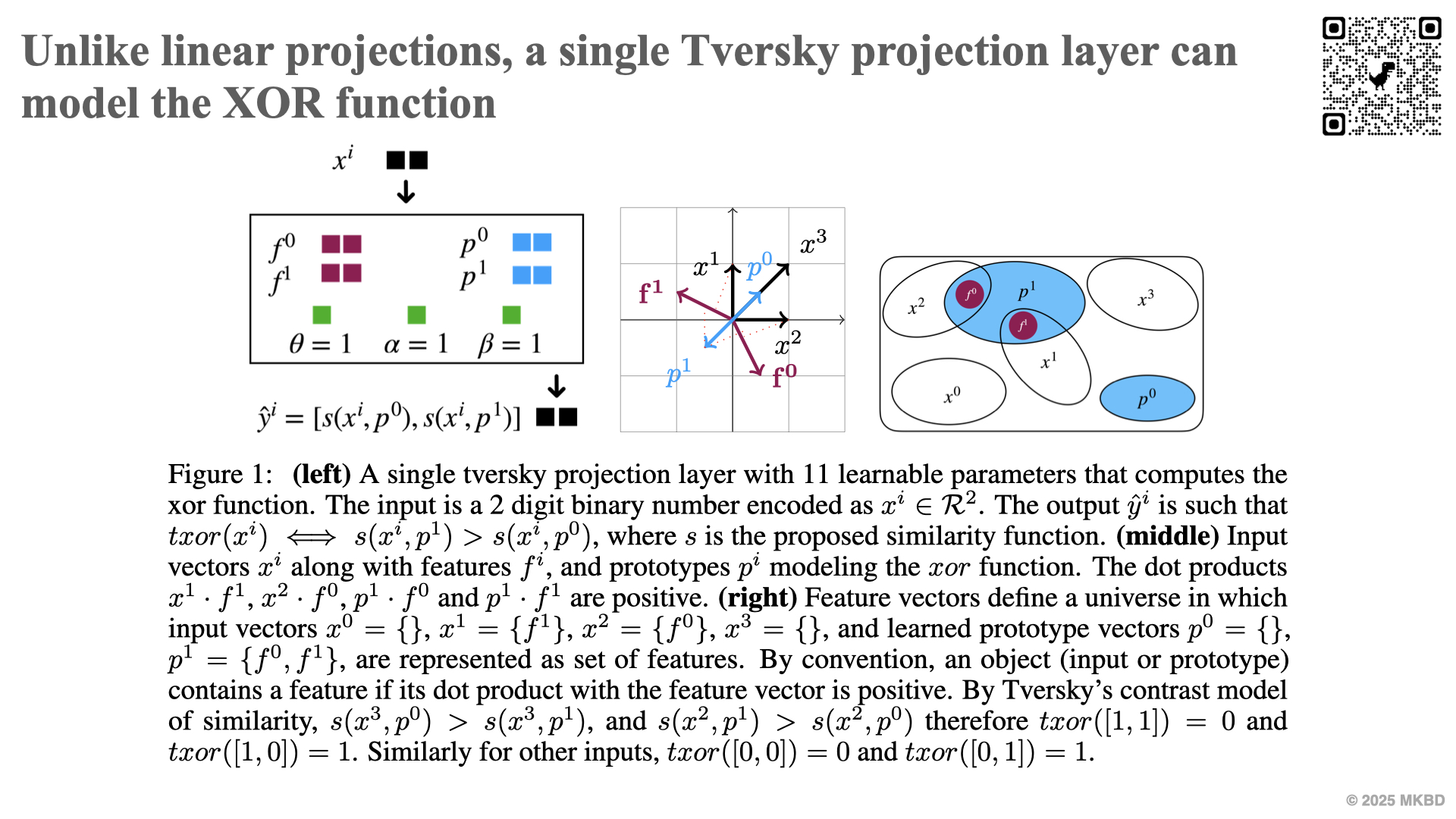
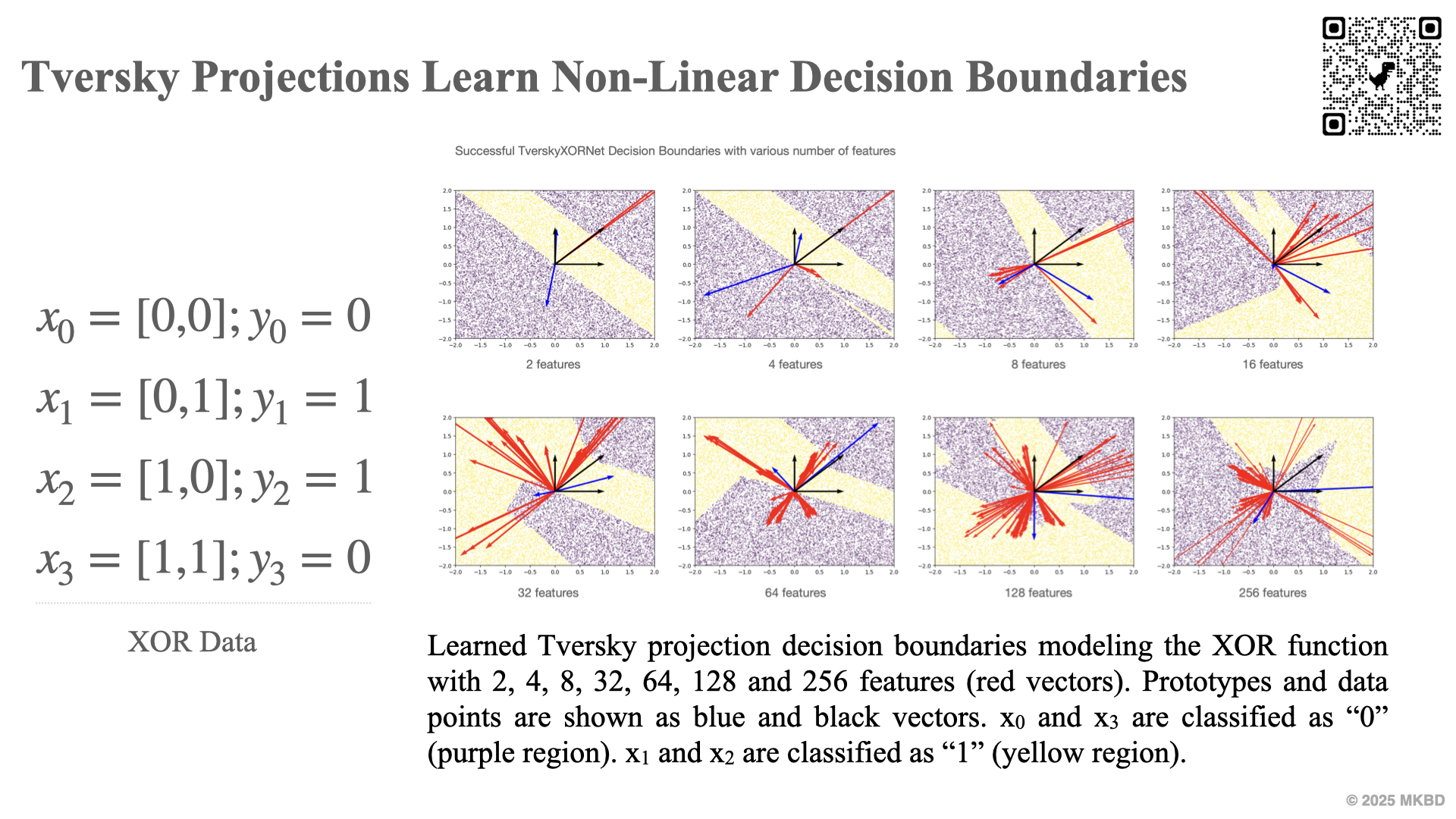
Both linear and Tversky projections compute the similarity of inputs to prototypes (respectively dot-product and Tversky similarity). Using this unified interpretation, we propose a novel method to visualize the parameters of both types of projections, highlighting the interpretability of Tversky neural networks.

See our paper for details.